Incremental Learning of Nonparametric Bayesian Mixture Models

April 15, 2021

by Gomes, Welling, Perona (CVPR 2008)

mixture-models dirichlet-process bayesian-nonparametrics clustering streaming online

Research Questions

• How to perform online/streaming inference in Dirichlet process mixture model?

Conceptual Notes

• Problem: Enumerating & updating all possible partitions (hypothesized clusters) requires superexponential time and space

• Idea:

  • Combine many clustering hypotheses into single set of constraints
  • For instance, if in every hypothesized partition, observations 1 and 2 are always grouped, then “clump” 1 and 2 together
  • each datapoint belongs to exactly 1 clump
  • the set of clumps is the partition with the fewest number of sets that can be unioned to construct every possible clustering hypothesis
  • Below, the first three rows are each one possible hypothesized partition. The final row are the clumps that can be used to construct every hypothesized partition

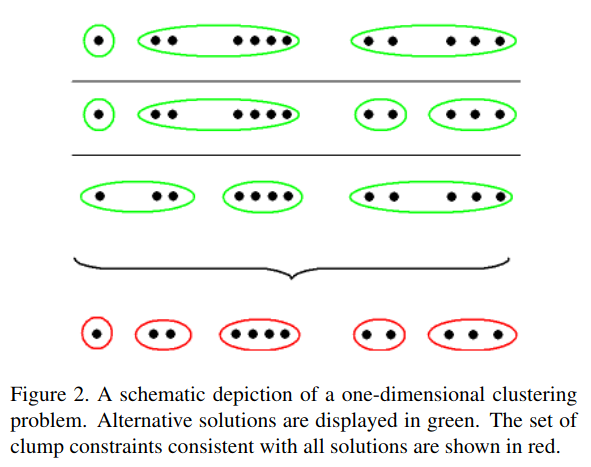
• Challenge: In theory, all partitions are valid hypotheses (although some partitions are more likely than others). Why prevents each clumps from containing exactly one point?
  • Answer: Unanswered. One relevant answer is they hard assign each data point to one cluster (equation 10) similarly to the Local MAP approximation:
  \[\argmax_k q(z_s = k)\]
• Challenge: How do we extract clump constraints without explicitly computing all hypothesized partitions?
  • Answer: Hypothesized partitions have redundancy in that they likely differ from each other only for a subset of points. “Our approach is to partition the clustering problem” into a series of independent subproblems […] This forms a tree of possible groupings of data and the bottom level of this tree defines our clump constraints.” I don’t understand this. For instance, in the below example, the tree seems to presume that all hypotheses can be split between the left 7 points and the right 5 points; what if no such cut exists?

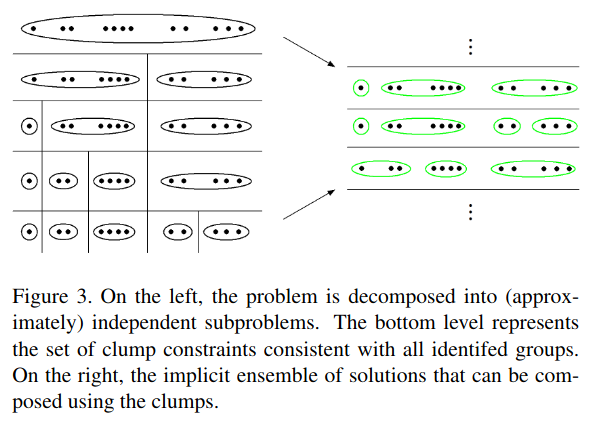
• Challenge: Relatedly, if not all partitions are valid hypotheses, then what how do we ensure unions of clumps yield a valid hypothesis? For instance, suppose we have clumps {1, 2}, {3}, {4} that arise from hypothesis {1, 2, 3}, {4} and hypothesis {1, 2, 4} {3}. But hypothesis {1, 2, 3, 4} is not a valid hypothesis.
  • Answer: Unanswered
• Challenge: The space of hypotheses, constructed from clump unions, is still combinatorically large. Do we actually get a benefit?

Algorithm Specifics

The algorithm is called the Memory Bound Variational Dirichlet Process (MB-VDP).

• Draw data in batches (called epochs) of size E data points
  • Compute best estimated mixture model using Blei and Jordan (2006) truncated variational Bayes model
    • Use a modified version from Kurihara 2007 that starts with one component and splits so long as ELBO / free energy increases
    • Perform variational optimization subject to clump constraints (how this constraint is imposed in the optimization is not clear)
  • Compression phase: compute clump constraints in top-down manner
    • Data points in same clump are used to update clump sufficient statistics
    • Unless too few points are in a clump to compute sufficient statistics (e.g. covariance). In this case, we save the individual data points (termed singlets)
    • Stop when too much time / space (number of clump constraints) used