Connections between Joint Embedding Self-Supervised Learning and Information Theory

Many methods in joint embedding self-supervised learning are directly inspired by or closely related to information theory. The general claim is that loss functions should maximize the mutual information between multiple views/augmentations/transformations of the same datum.

TODO: Read these papers from Rodriguez-Galvez et al. (ICML 2023):

Small batch sizes degrade the performance of MVSSL methods, especially contrastive ones (Chen et al., 2020a; Grill et al., 2020; Caron et al., 2021). Potentially, this is due to the fact that most meth- ods maximize the entropy either explicitly or implicitly, as shown in this paper, and the entropy estimation is limited to log k bits for a batch size of k (McAllester & Stratos, 2020). Some works (HaoChen et al., 2021; Chen et al., 2021; Yuan et al., 2022) addressed this issue and modified existing meth- ods to perform well under the small batch size regime

Maximizing Mutual Information Insufficient For Learning Good Representations

Mutual information is invariant under arbitrary invertible transformations, meaning maximizing mutual information has little-to-no incentive to avoid learning highly entangled representations. Additionally, mutual information is difficult to estimate in practice, and so many methods use surrogates. Based on these observations, Tschannen, Djolonga et al. (ICLR 2020) questioned whether an information-theoretic view of JESSL can explain its success. The authors argued that maximizing mutual information is insufficient for learning good representations. The authors focus on two mutual information estimators:

1. InfoNCE:

\[I(X ; Y) \geq \mathbb{E} [ \frac{1}{K} \sum_{i=1}^K \log \frac{\exp f(x_i, y_i)}{\frac{1}{K} \sum_{j=1}^K exp f(x_i, y_j)} ]\]

where \(f()\) is a “critic” that tries to predict the \(y\) that \(x\) corresponds to, i.e., is paired with.

1. NJW:

\[I(X ; Y) \geq \mathbb{E}_{p(x, y)}[f(x, y)] - \exp(-1) \mathbb{E}_{x \sim p(x), y \sim p(y)}[\exp(f(x,y))]\]

InfoNCE is maximized by $$f^*(x, y) = \log p(y

x)\(and NJW is maximized by\)f^*(x, y) = 1 + \log p(y

x)$$.

Evidence 1: Bijective Encoders Fix Mutual Information But Improve Downstream Classification

Experiment:

• Learn representations for top half of MNIST images (similar results for CIFAR10)
• Network is RealNVP with 30 coupling layers
• Train a linear classifier on the representations: 89% accuracy
• Baseline:
  • Linear classifier on pixel space: 85% accuracy
  • Supervised MLP / ConvNet: 94% accuracy

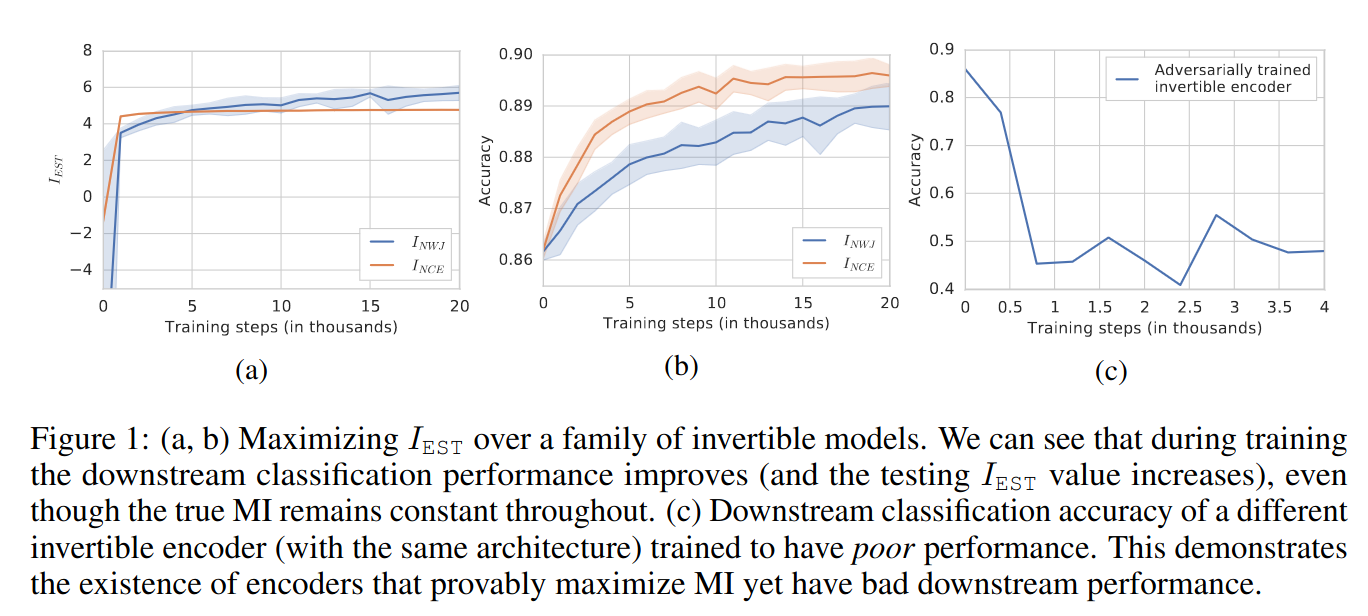
Rylan’s comments:

• The main result (a network constrained such that MI must be constant for all parameters but achieves better downstream linear classification accuracy) is correct
• But the experimental methodology seems odd
  • This top half/bottom half data augmentation seems quite different from the standard JESSL setup
  • Using MNIST and one architecture (RealNVP) makes it difficult to generalize to other datasets, architectures and augmentations
  • Accuracy is a metric I generally try to avoid
  • The accuracy is barely better than a linear classifier on pixel space
  • The y axis scaling for \(I_{EST}\) might not be linear.

Maybe the takeaway from this result is that this particular top half/bottom half augmentation doesn’t correspond to

Evidence 2: Maximizing Mutual Information Can Hurt Downstream Classification

Experiment:

• Train a bijective representation to maximize MI and minimize downstream linear classification (trained adversarially)

Evidence 3:

Entropy & Reconstruction in JESSL

Rodriguez-Galvez et al. (ICML 2023) later studied the relationship between mutual information and 3 families of JESSL methods: (1) Contrastive methods, e.g., SimCLR, (2) Clustering methods, e.g., SwAV and (3) Distillation methods, e.g., BYOL.

The authors specifically studied the “entropy and reconstruction” (ER) lower bound:

\[I(Z_1; Z_2) \geq H[Z_2] + \mathbb{E}_{Z_2} [\log q(Z_1 | Z_2)]\]

Rodriguez-Galvez et al. showed that:

1. None of the three families directly maximize the ER lower bound, but instead approximate it
2. Clustering-based methods approximately maximize the ER lower bound
3. Distillation-based methods don’t maximize entropy but ensure it does not collapse

The authors propose training with an ER-based loss, using a KDE-based entropy estimator:

\[\begin{align*} \hat{p}(z) &= \frac{1}{N} \sum_{n=1}^N k(\frac{z - z_n }{h}) \\ \hat{H}[Z] &= - \sum_{n=1}^N \hat{p}(z_n) \log \hat{p}(z) \end{align*}\]

for kernel function \(k\) with bandwidth \(h\). Oddly, Rodriguez-Galvez et al. found that training with ER yields the same or slightly worse downstream performance. However, the networks trained with ER are more robust.

The below plot from Rodriguez-Galvez et al. ICML 2023 bites into the Tschannen et al. ICLR 2020 paper. Specifically, there is no clear relationship between reconstruction, entropy and downstream linear classification performance.