Paper Summary - "Universal Hopfield Networks"

The below are my notes on Millidge et al. 2022’s Universal Hopfield Networks.

Summary

• Associative memory models consider the challenge of storing and retrieving memories
• Many neural network associative memory models have been proposed, including Hopfield Networks Sparse Distributed Memories and modern continuous Hopfield networks
• This paper proposes a general framework for understanding different associative memory models
• This paper also demonstrates that each model has a corresponding energy function that is a Lyapunov function of the dynamics
• This paper then empirically investigates the capacity of different models

Universal Hopfield Networks

• Many (all?) associative memory models can be understood with three steps:
  • Similarity: The input is compared to previous patterns
  • Separation: The similarity scores are separated
  • Projection: The similarity scores are used to determine what information to retrieve

Hopfield Networks

\[z = sign(M^T identity(M q))\]

Sparse Distributed Memories

\[z = P thresh(hamming(M, q))\]

Modern Continuous Hopfield Networks

\[z = W^T softmax (W q)\]

Continuous Sparse Distributed Memories

\[z = P softmax (A q)\]

Auto-associative vs Hetero-associative Memories

If the project matrix \(P\) is the same as \(M\), then a memory model is called auto-associative; if the two are different, then the memory model is called hetero-associative.

Relation to Transformer Networks

A hetero-associative Modern Continuous Hopfield Network is equivalent to a self-attention layer:

\[z = V softmax(K q)\]

Neural Dynamics

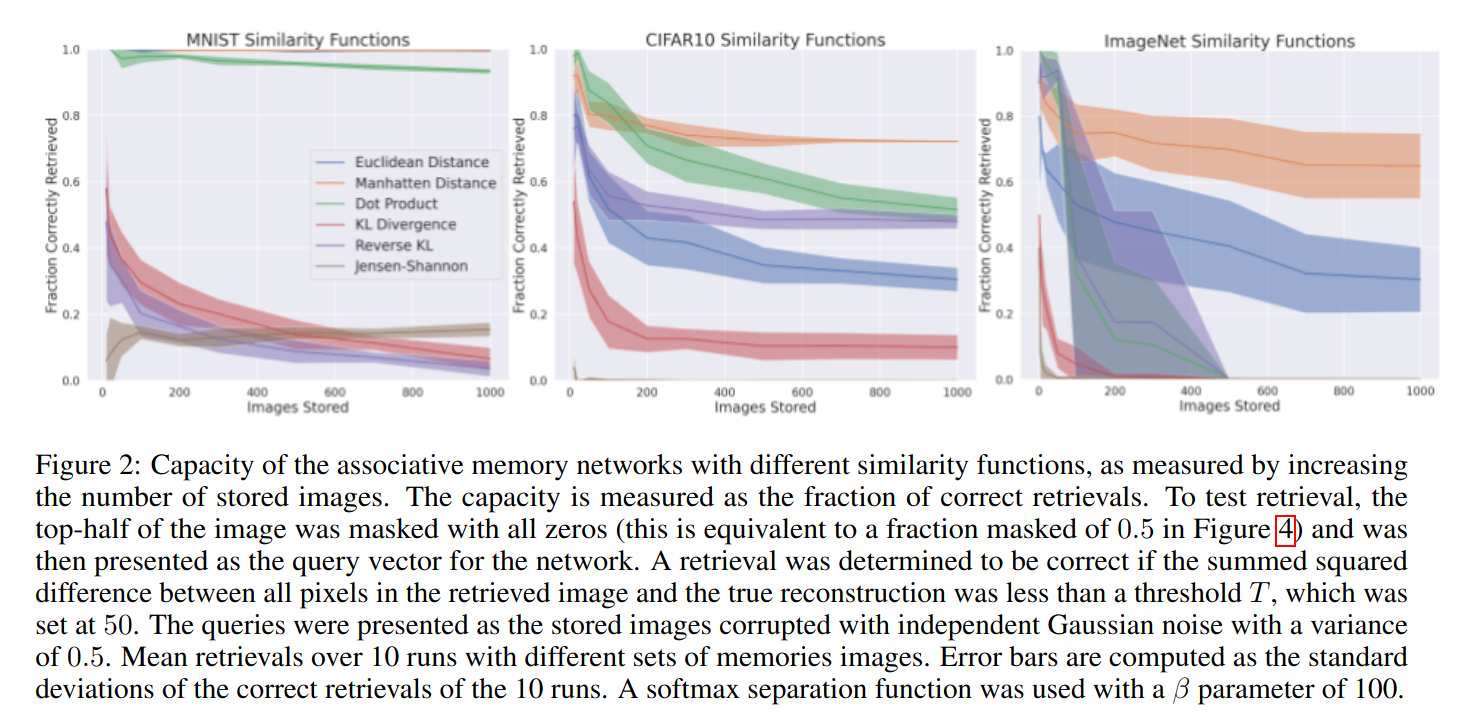
Experiments

Using the dot product for similarity performs more poorly than using a Manhattan or Euclidean distance.