Variational Inference for Dirichlet Process Mixtures
Research Questions
- How to perform variational inference in Dirichlet Process (DP) Mixture Model?
Background
For a quick primer on Dirichlet processes and their use in mixture modeling, see my notes on DPs
Approach
Assuming the observable data is drawn from an exponential family distribution and the base distribution is the conjugate prior, we have a nice probabilistic model:
- Draw \(V_i \lvert \alpha \sim Beta(1, \alpha)\). Let \(\underline{V} = \{V_1, V_2, ...\}\)
- Draw parameters for the mixing distributions \(\eta_i^* \lvert G_0 \sim G_0\), where \(G_0\) is the base measure of the DP. Let \(\underline{\eta^*} = \{\eta_1^*, \eta_2^*, ...\}\).
- For the \(n= 1, ..., N\) data point
- Draw \(Z_n \lvert \underline{V} \sim Multi(\pi(V))\)
- Draw \(X_n \lvert Z_n \sim p(x_n \lvert \eta_{z_n^*})\)
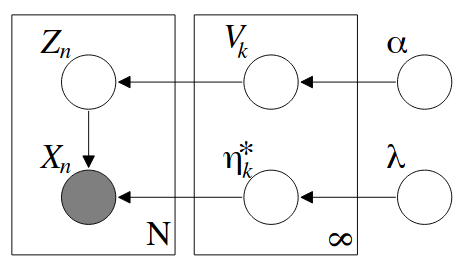
In constructing the variational family, we take the usual approach of breaking dependencies between latent variables that make computing the posterior difficult. Our variational family is
\[q(\underline{V}, \underline{\eta^*}, \underline{Z}) = \prod_{k=1}^{K-1} q_{\gamma_k}(V_k) \prod_{k=1}^K q_{\tau_k}(\eta_t^*)\prod_{n=1}^N q_{\phi_n}(z_n)\]where \(K\) is the variational truncation of the number of mixing components and \(\{\gamma_k\} \cup \{\tau_k\} \cup \{\phi_n \}\) are our variational parameters.