Paper Summary - "Imitation with Neural Density Models"

The below are my notes on Kim et al. 2021’s Imitation with Neural Density Models.

Summary

• Proposes a framework for Imitation Learning by combining:
  • density estimation of expert’s occupancy measure, and
  • Maximum Occupancy Entropy RL with density as the reward
• Proposes an imitation learning algorithm, Neural Density Imitation (NDI)

Background

• Imitation Learning (IL) aims to learn optimal behavior by mimicking expert demonstrations
• Many IL approaches try to minimize a statistical distance between state-action distributions (i. the “occupancy measures” \(\rho_{\pi_E}\) and \(\rho_{\pi_{\theta}})\)

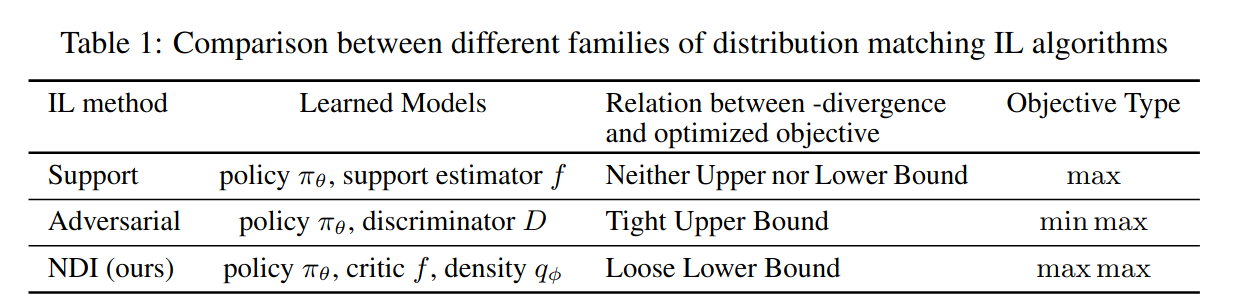
Method

• 2-Phase Approach
• First, Learn a density estimate \(q_{\phi}\) of the expert’s occupancy measure \(\rho_{\pi_{E}}\)
• Second, use Maximum Occupancy Entropy RL (MaxOccEntRL) i.e. use the density estimate \(q_{\phi}\) as a fixed reward for RL and maximizes the occupancy entropy \(H[\rho_{\pi_{\theta}}]\)
• The objective is:

\[\mathbb{E}_{\rho_{\pi_{\theta}}}[\log q_{\phi}(s, a)] + H[\rho_{\pi_{\theta}}]\]

• MaxOccEntRL applies regularization to the occupancy measure instead of the policy, whereas MaxEntRL only applies to the policy

Challenges

• The expert occupancy measure \(\rho_{\pi_E}\) is unknown and must be estimated from demonstrations
• The entropy \(H[\rho_{\pi_{\theta}}]\) may not exist in closed form, especially if \(\rho_{\pi_{\theta}}\) is an implicit density

Estimating the Expert Occupancy Measure

• Goal: Learn a parameterized density model \(q_{\phi}(s, a)\) of \(\rho_{\pi_{E}}\) from samples
• Approach: Try autoregressive models and energy-based models (EBMs)

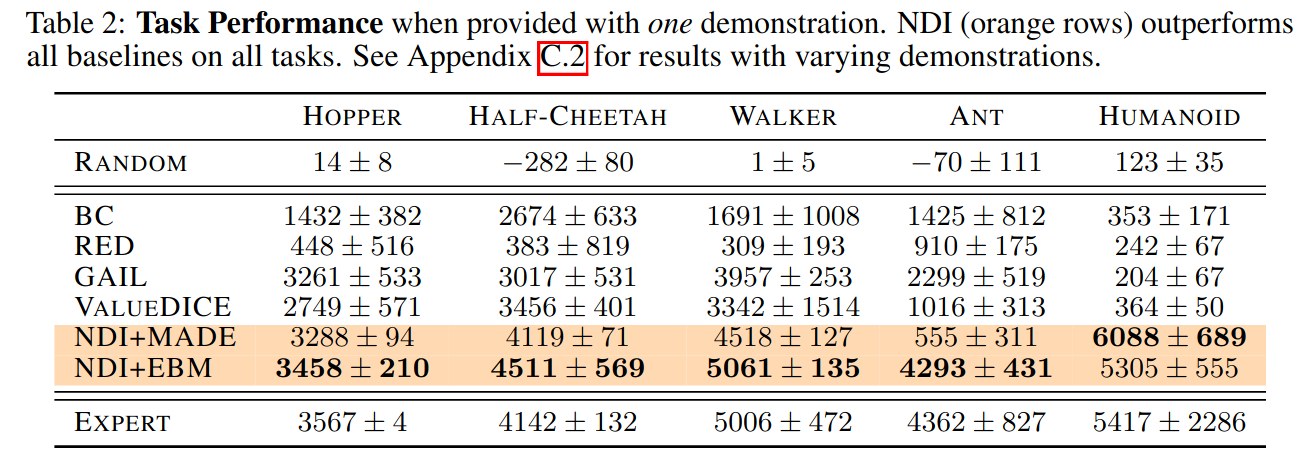
Results