Cheatsheet - Self-Supervised Learning for Vision

Method	Latent Dim	Batch Size	Optimizer	Learning Rate	Weight Decay	Scheduler	Epochs
SimCLR	128	4096	LARS	4.8	1e-6	Linear Warmup, Cosine Decay	100
TiCo	256	4096	LARS	3.2	1.5e-6	Linear Warmup, Cosine Decay	1000
VICReg	8192	2048	LARS	1.6	1e-6	Linear Warmup, Cosine Decay	1000

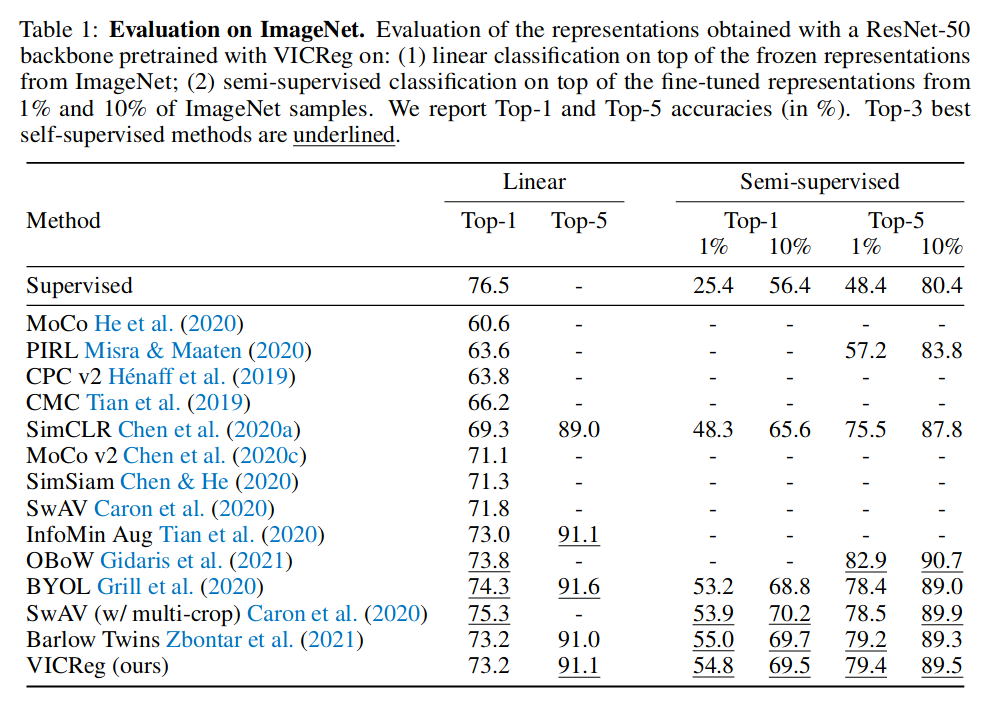
Figure from VICReg (ICLR 2022):

CPC (Arxiv 2018)

Deep InfoMax (DIM) (ICLR 2019)

AMDIM (NeurIPS 2019)

MoCo (CVPR 2020)

SimCLR (ICML 2020)

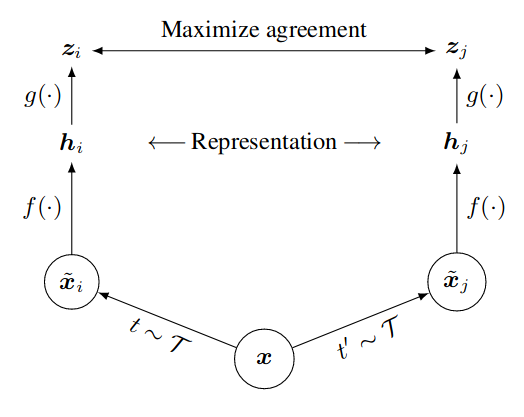
• 3 data augmentations, applied sequentially: random cropping, random color distortions, random Gaussian blur
• Base encoder \(f(\cdot)\)
• Projection head \(g(\cdot)\); specifically use a 1-hidden-layer MLP
• Normalized temperature-scaled Cross Entropy (NT-Xent) loss:

\[\ell_{i, j} = -\log \frac{\exp (sim(z_i, z_j) / \tau)}{\sum_k^{2N} \mathbb{1} \exp (sim(z_i, z_k) / \tau)}\]

• Uses only augmented data in the batch
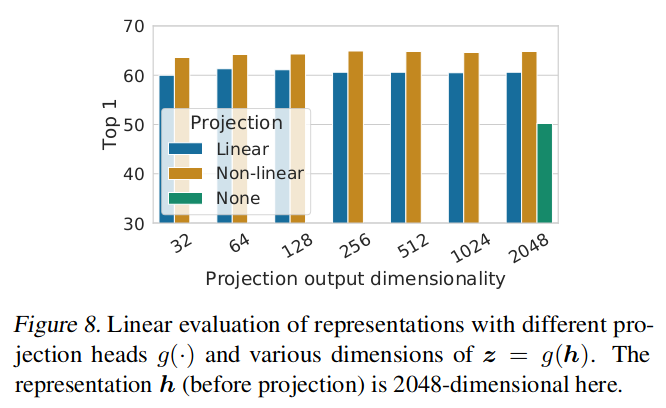
• No projection significantly hurts performance; why?

• Paper claims that using \(h_i\) rather than \(z_i\) is better, but I don’t see in what sense, or where the evidence is?
• NY-Xent loss outperforms logistic loss and margin loss
• Another nice graphic from TiCo

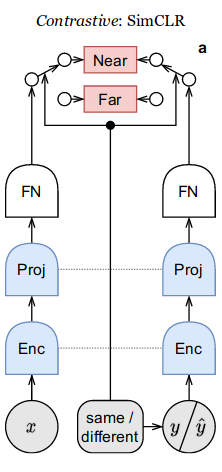
SwAV (NeurIPS 2020)

BYOL (NeurIPS 2020)

SimSiam (CVPR 2021)

• No negative sample pairs, no large batches, no momentum encoders

W-MSE

• Whitening Mean-Squared Error

• Criticism: matrix inversion is slow and possibly numerically unstable
• Criticism: Whitening operator is estimated over multiple batches, and may have high variance

TiCo (Rejected at NeurIPS 2021)

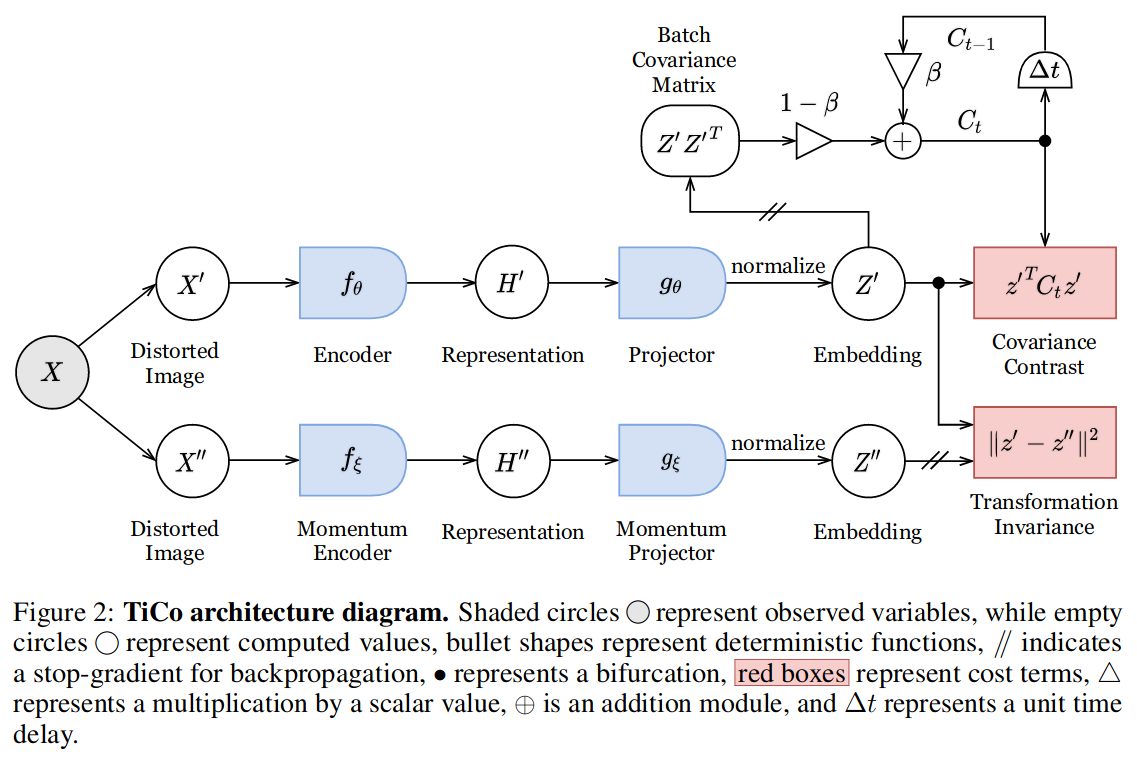
• Loss has 2 terms: transformation invariance and covariance contrast

\[\ell = -\frac{1}{N} \sum_n ||z_n^' z_n^{''}||_2^2 + \frac{\rho}{N} \sum_{n} (z_n^')^T C_t z_n^'\]

where \(C_t\) is the second moment matrix of the representations.

Equivalently:

\[\ell = -\frac{1}{N} \sum_n z_n^{'} \cdot z_n^{''} + \frac{\rho}{N^2} \sum_{ij} (z_i^{'} \cdot z_j^{''})^2\]

• TiCo is both a contrastive and redundancy reduction method
• The covariance contrast loss incentivizes (transformations of) different data to be orthogonal
• The covariance contrast loss can also be viewed as regularizing the Frobenius (matrix norm) of \(\frac{1}{N} Z_{F}^T Z_F\) where \(Z_F\) is the \(N \times F\) matrix of normalized features

VICReg (ICLR 2022)

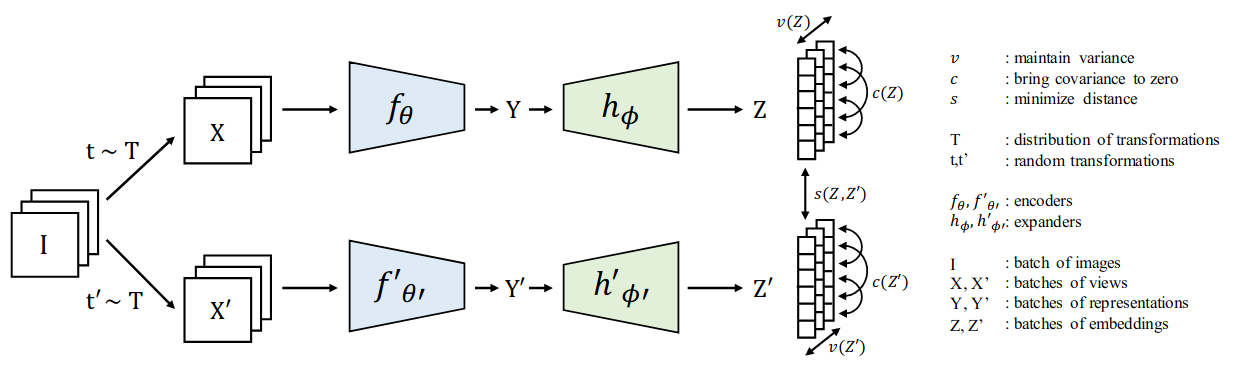
• VICReg = Variance-Invariance-Covariance Regularization
• Avoids collapse by (1) maintaining variance of each embedding dimension above a threshold and (2) decorrelating each pair of variables
• Invariance loss:

\[\ell = \frac{1}{N} \sum_n ||z_n^{'} - z_{n}^{''}||^2\]

• Variance regularization loss:

\[\ell = \frac{1}{D} \sum_d \max(0, \gamma - S(z_d, \epsilon))\]

where $S(x, \epsilon) = \sqrt{\mathbb{V}[x] + \epsilon}$

• Using the standard deviation, not the variance, is critical for ensuring the gradient isn’t too small
• Covariance regularization loss:

\[\ell = \frac{1}{N - 1} \sum_n (z_n - \bar{z}_n) (z_n - \bar{z}_n)^T\]

• Encourages off-diagonal elements of covariance to be close to 0
• Decorrelation at embedding level had a decorrelation effect at the representation level
• Standardization of embeddings hurts performance very slightly (0.2%), but removing standardization in the hidden layers hurts performance (1.2%)
• Results:

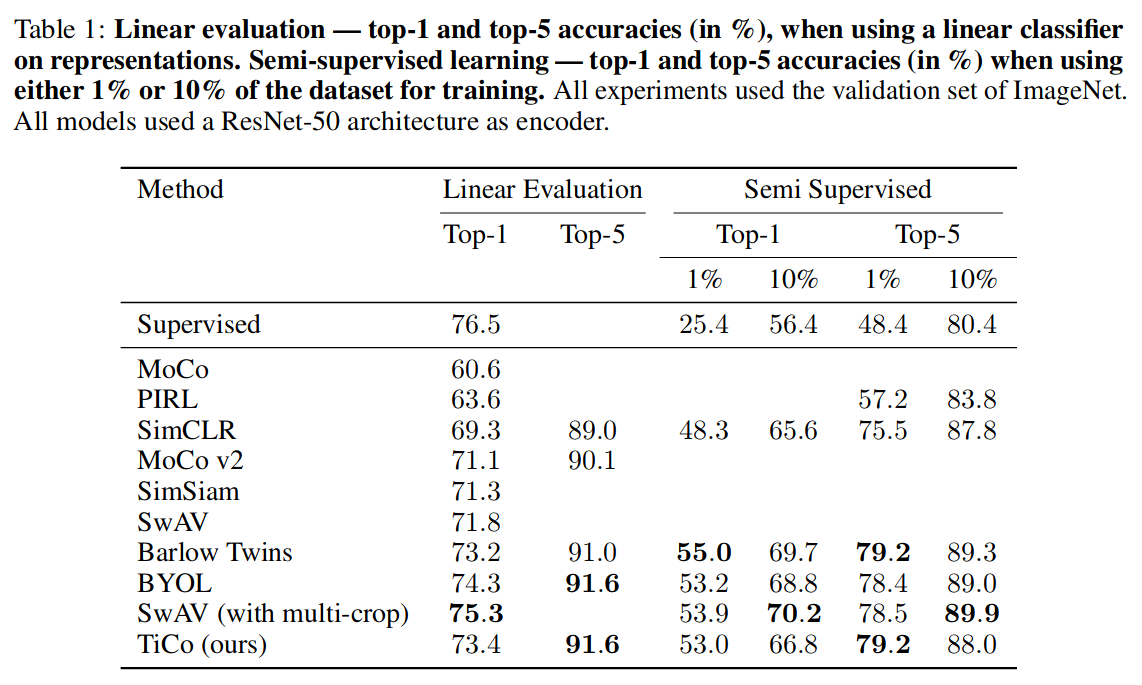
Barlow Twins