Hollow Spheres in High Dimensions

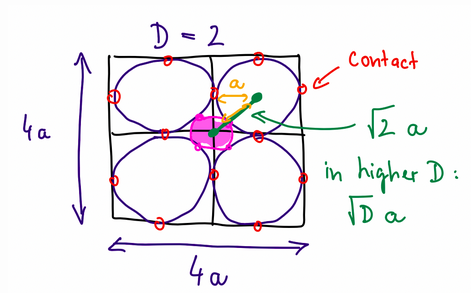
Stan just wrote a post about the counter-intuitive properties of high dimensions, focusing on a sphere touching surrounding spheres packed inside surrounding squares:

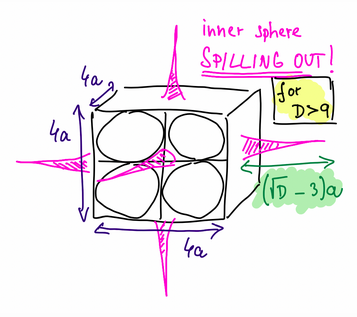
He then shows as the dimensionality increase, the inner sphere becomes this spiky object, popping out from between the surrounding spheres:

It’s a common example, but one that (in my opinion) is too complicated to explain simply, especially when there’s a much simpler example available: a single sphere. Let’s ask a simple question: how much of a sphere is close to its boundary in high dimensions?

Dimensions = 2

Let’s start with \(D=2\) dimensions and ask what fraction of a radius-\(r\) sphere (i.e. a circle) is within \(\epsilon << r\) of its surface. We know that the total volume is \(\pi r^2\) and the inner volume is \(\pi (r - \epsilon)^2\), so the fraction not near the periphery is:

\[\frac{\pi (r - \epsilon)^2}{\pi r^2} = \Big(\frac{r - \epsilon}{r}\Big)^2\]

For a small \(\epsilon\) e.g. 0.01r, a high fraction of the volume is in the middle e.g. 98%. and so most of the circle is not near the surface.

Dimensions = 3

In \(D=3\) dimensions, we again ask: what fraction of a radius-\(r\) sphere is within \(\epsilon < r\) of its surface. We know that the total volume is \(\frac{4}{3}\pi r^3\) and the inner volume is \(\frac{4}{3} \pi (r - \epsilon)^3\), so the fraction not near the surface is:

\[\frac{\frac{4}{3} \pi (r - \epsilon)^3}{\frac{4}{3} \pi (r)^3} = \Big(\frac{r - \epsilon}{r}\Big)^3\]

Again, most of the volume is in the middle, and so most of the sphere is not near the boundary.

Dimensions = D

What happens as the number of dimensions grow? We find that the volume in the center of the n-sphere is given by

\[\Big( \frac{r-\epsilon}{r} \Big)^D\]

As \(D\) gets larger, that fraction converges to 0 since the term being exponentiated, \((r-\epsilon) / r\) is less than \(1\). Consequently, the fraction of the sphere in the middle goes to zero and the sphere becomes hollow! In 2D, almost all of a circle is more than \(\epsilon\) away from its shell, but in high dimensions, almost all of an n-sphere is within \(\epsilon\) from its boundary.

To summarize: spheres in high dimensions become hollow!!

So much simpler than boxes, spheres and spikes!!