Pretraining Scaling Laws for Generative Evaluations of Language Models

Authors: Rylan Schaeffer\(^*\), Noam Levi\(^*\), Brando Miranda, Sanmi Koyejo

\(^*\) Equal contribution

Venue: ICLR 2026

Quick Links

• Paper
• Poster
• Tweeprint

Summary

Scaling laws for pretraining loss and discriminative benchmarks are well established. But what about generative tasks like math problem-solving?

We propose and rigorously evaluate three scaling laws for predicting pass-at-\(k\) on generative benchmarks (GSM8K, MATH).

1/N

---

Our first scaling law fits pass-at-\(k\) as a function of pretraining compute:

\[-\log(\mathrm{pass}@k) = E_0(k) + C_0(k) \cdot C^{-\alpha(k)}\]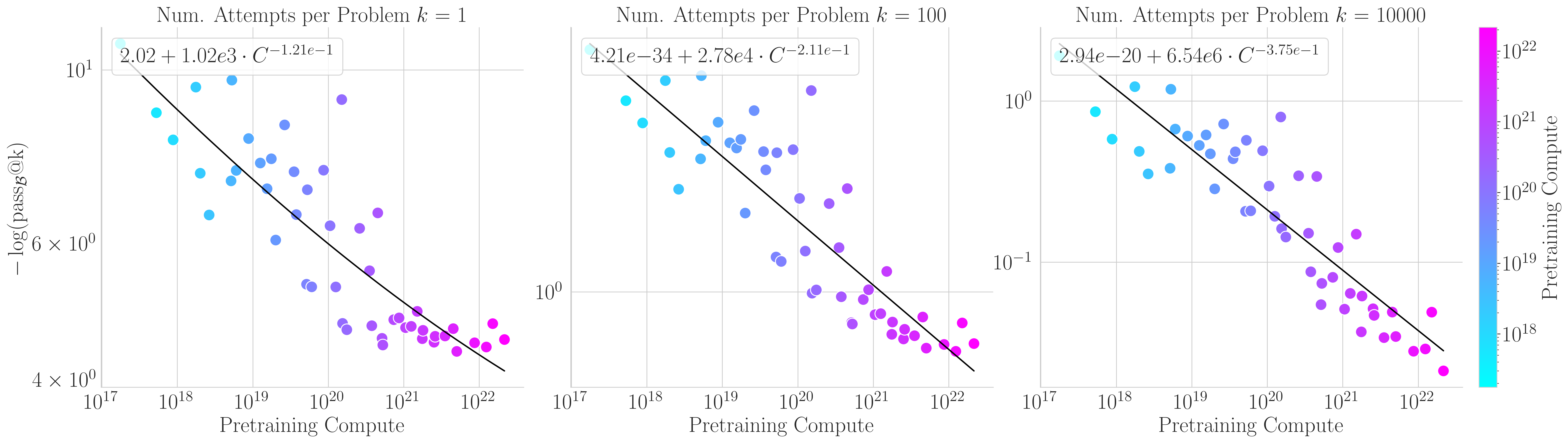

2/N

---

A key discovery: the number of attempts \(k\) isn’t just a metric parameter—it’s a control lever that shapes the entire scaling law.

As \(k\) increases: irreducible error vanishes, and the scaling exponent steepens from ~0.12 to ~0.38.

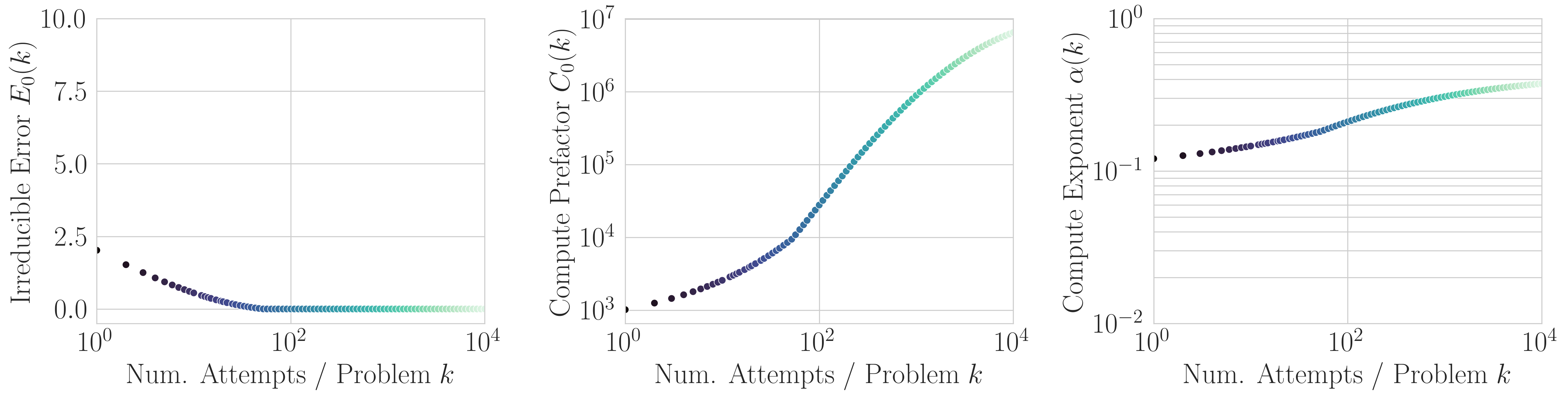
3/N

---

Our second scaling law decomposes compute into parameters \(N\) and tokens \(D\):

\[-\log(\mathrm{pass}@k) = \mathcal{E}_0(k) + N_0(k) \cdot N^{-\beta(k)} + D_0(k) \cdot D^{-\gamma(k)}\]

This yields tighter in-range fits but similar predictive performance.

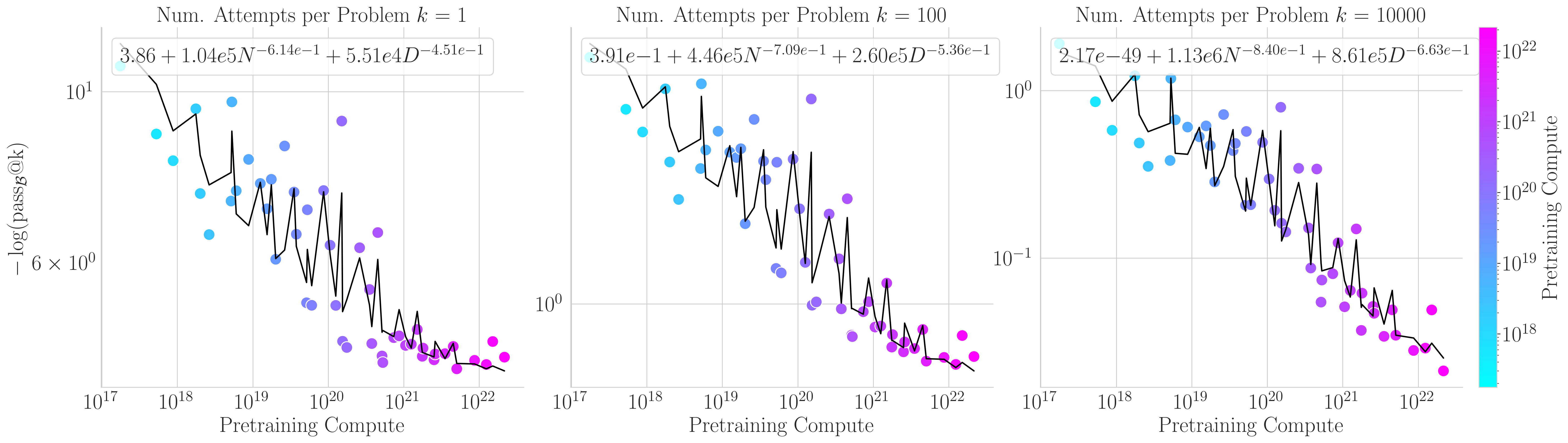
4/N

---

Our third scaling law uses gold reference likelihoods—how likely the model thinks the ground-truth solution is:

\[-\log(\mathrm{pass}@k) = \xi_0(k) + K_0(k) \cdot [-\log(\mathrm{GoldProb})]^{\kappa(k)}\]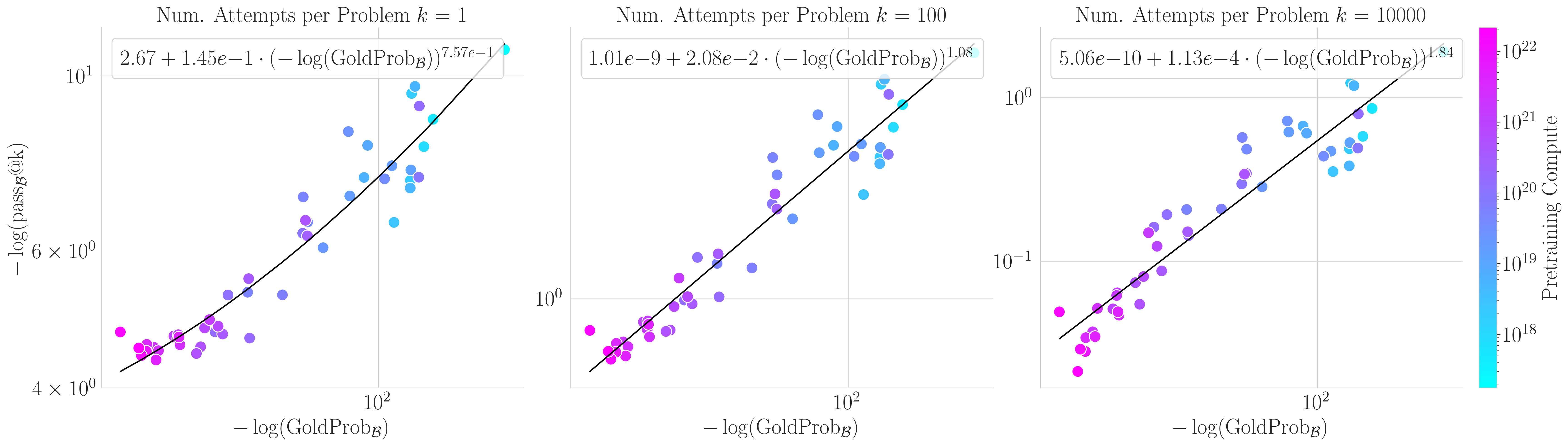

5/N

---

How predictive are these laws? We backtest: fit on cheap models, predict expensive models.

The compute and params+tokens laws require models within ~2 orders of magnitude of the target.

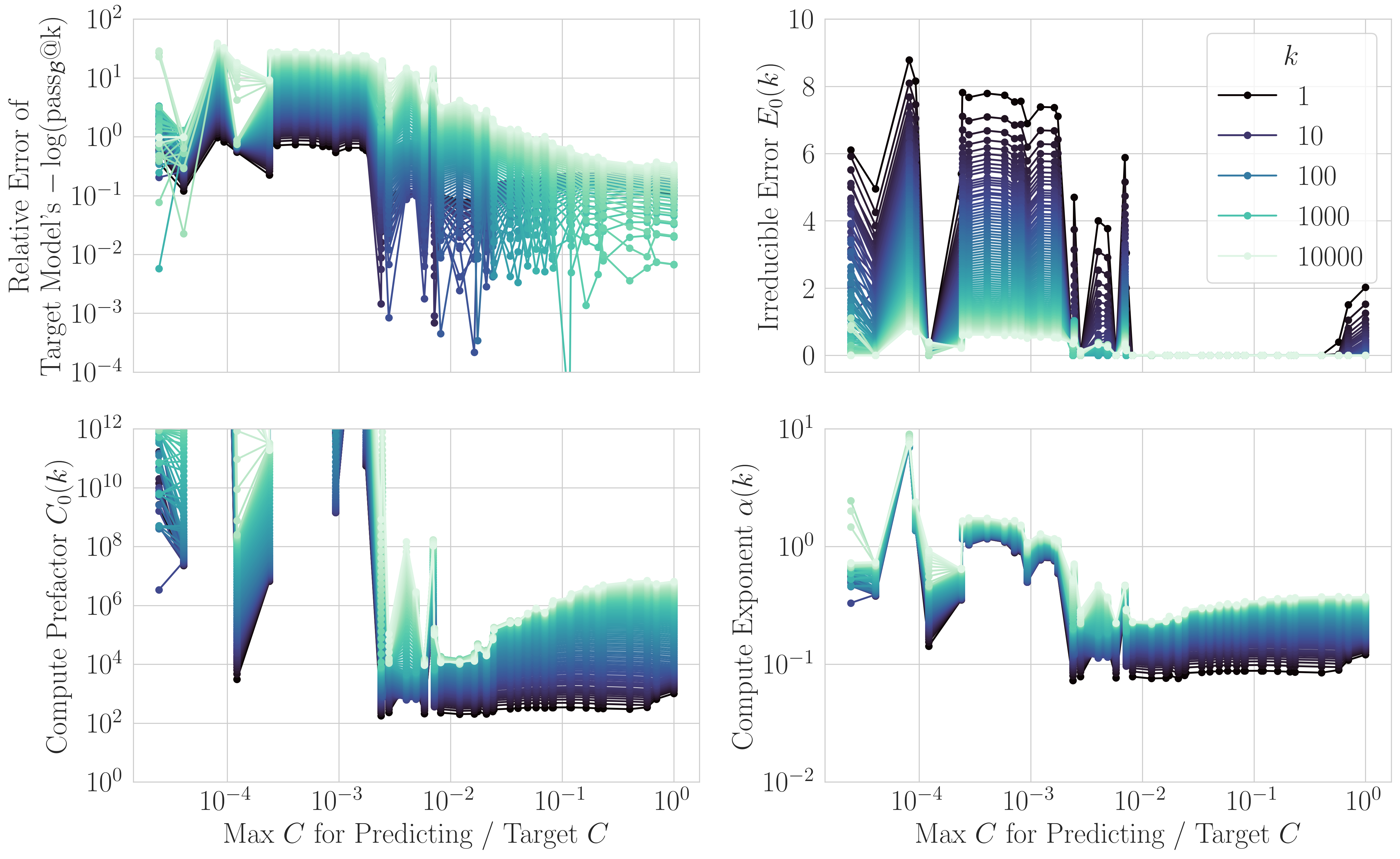
6/N

---

The gold reference law is remarkably stable—parameters converge using models up to ~5 orders of magnitude cheaper than the target.

This suggests gold reference likelihoods provide a robust signal for long-range forecasting.

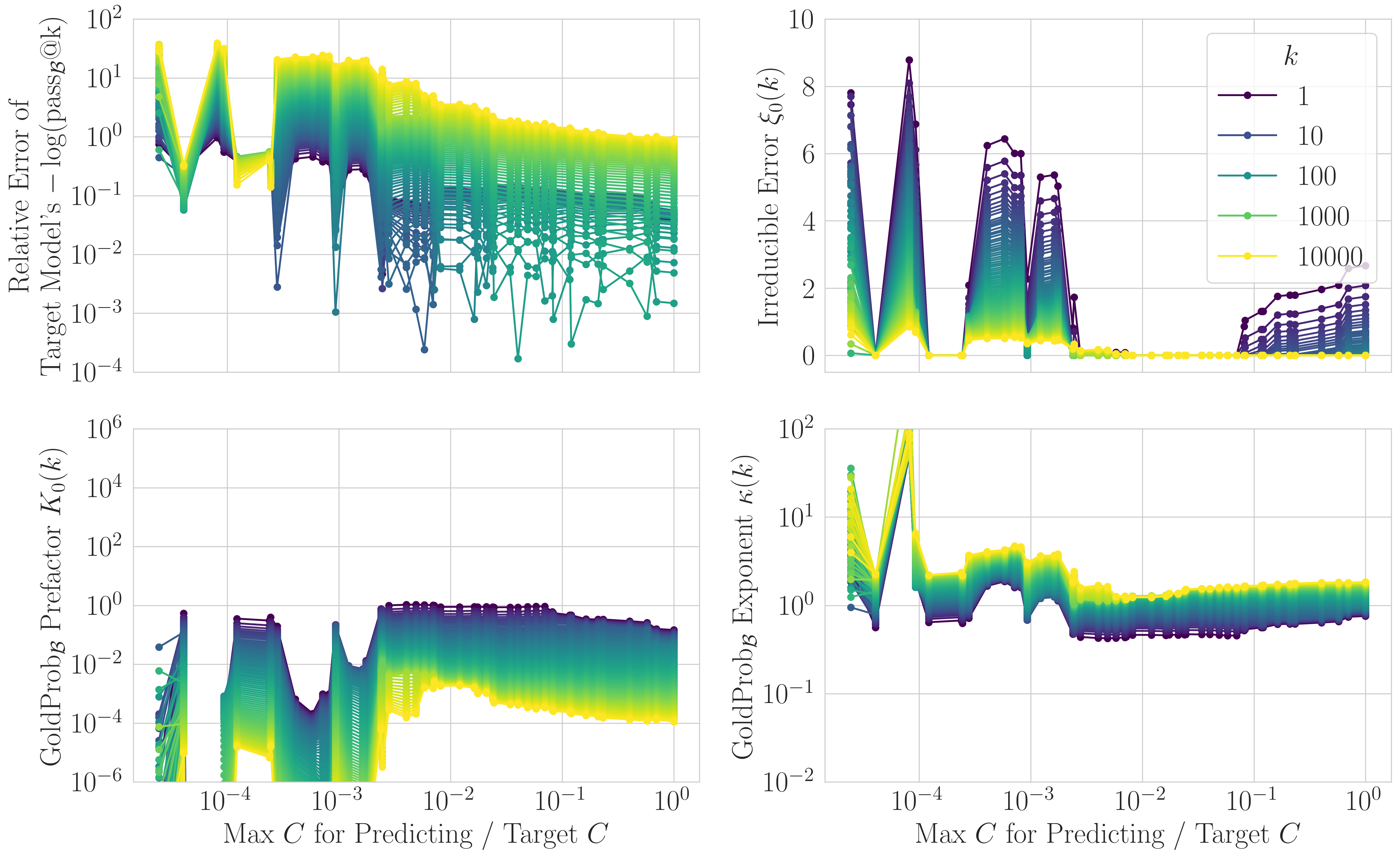
7/N

---

We prove a theoretical connection: the compute law is the compute-optimal envelope of the params+tokens law.

Deviating from optimal allocation introduces a multiplicative penalty. This quantifies exactly how much “effective compute” you lose by over/undertraining.

8/N

---

Key takeaways:

• Pass-at-\(k\) follows predictable scaling laws
• \(k\) is a powerful lever that eliminates irreducible error and steepens scaling
• Gold reference likelihoods are uniquely stable across 5 OOM
• Compute scaling emerges as the optimal envelope of params+tokens scaling

9/N